La película El Hombre que conocía el infinito,
actualmente en cartelera, retrata la vida del matemático indio
Srinivasa Ramanujan, que sin estudios ni formación asombró a los
eruditos de la Universidad de Cambridge con sus series del número π. Un
siglo después, otro matemático autodidacta y enamorado de este número
tan especial, el zaragozano Jesús Guillera, destaca el legado de su
colega y los nuevos desafíos que plantean las fórmulas.
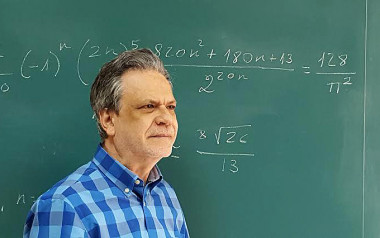
Jesús Guillera es colaborador extraordinario del departamento de Matemáticas de la Universidad de Zaragoza. / J. Guillera
Por Enrique Sacristán
El actor Dev Patel, famoso por protagonizar Slumdog Millionaire, da vida a Ramanujan en El Hombre que conocía el infinito. La
película refleja la pobreza en la que vivía el genial matemático indio
Srinivasa Ramanujan (1887-1920) en Madrás antes de ser admitido en la
Universidad de Cambridge.
En España hay un matemático cuyos trabajos
sobre las fórmulas del número pi guardan paralelismos con los de
Ramanujan. Él es Jesús Guillera, que ha comentado con Sinc el
largometraje sobre su predecesor indio.
¿Qué le ha parecido la película?
La
vi con algunos familiares y a todos nos gustó. Nos pareció una historia
muy bonita y bien contada. Además, las fórmulas que se muestran de
Ramanujan son correctas, ya que uno de los asesores del guionista ha
sido el matemático estadounidense Ken Ono. No sé si en España se ha promocionado desde el mundo académico, pero en Reino Unido, por ejemplo, lo ha hecho Manjul Bhargava (Medalla Fields 2014) en Oxford.
“Al igual que él investigué durante mucho tiempo en solitario y de forma autodidacta, cuando era profesor en un instituto”.
¿Qué destacaría de la figura de Ramanujan?
Me
impresionan sus extraordinarias identidades matemáticas descubiertas de
forma autodidacta y sin tener apenas estudios previos, aunque me
sorprende su creencia de que era una diosa quien le dictaba las fórmulas
mientras dormía. De sus cualidades sobresale su extraordinaria
intuición, creatividad, ingenio, destreza y rapidez de cálculo;
características propias del gran genio matemático que fue y que pueden
apreciarse en sus numerosas y maravillosas identidades y fórmulas a las
que llegó sin elaborar complicadas teorías abstractas. En unos cuadernos
escribía sus ingeniosos resultados sin las demostraciones, aunque se
han logrado después.
¿Qué paralelismos encuentra entre su caso y el suyo?
Aunque
Ramanujan casi no tenía estudios y yo me licencié en Físicas, al igual
que él investigué durante mucho tiempo en solitario y de forma
autodidacta. En su caso remitió una carta a G. H. Hardy de la
Universidad de Cambridge y luego colaboraron juntos en Inglaterra. Por
mi parte envíe un email a D. Zeilberger de la Universidad Rutgers (EE
UU) con dos de mis fórmulas y un artículo con las demostraciones, que
publicamos luego en la revista Advances in Applied Mathematics. Además, en ambos casos hemos presentado fórmulas para obtener decimales del número π.
Cartelera de la película sobre Ramanujan y foto real del matemático indio. / Oberwolfach Photo Collection
¿Y las diferencias?
Mis descubrimientos
son interesantes y notables pero mi obra no es comparable ni de lejos
con la del genio Srinivasa Ramanujan, ni en extensión, ni en variedad
(se dedico a mucho más que al número pi); teniendo en cuenta, además, su
corta vida, ya que murió de tuberculosis a los 32 años. Otra diferencia
es que yo no podría realizar mis investigaciones si no fuera porque hoy
tenemos ordenadores, con los que puedo explorar y poner a prueba mis
ideas, que se me suelen ocurrir de noche. Luego, de día, escribo los
artículos. Uno de los programas que utilizo es el algoritmo WZ
desarrollado por Wilf y Zeilberger, por el que recibieron el prestigioso
Premio Steele.
¿Cuántos decimales de π se pueden conseguir mediante fórmulas?
Se
van obteniendo por grupos. La mejor de las once fórmulas que he
publicado da cinco decimales de pi por término sumado, pero una de las
de Ramanujan ofrece ocho, y los hermanos ucranianos Chudnovsky
obtuvieron lo que se denomina la más ‘rápida’: una que da los decimales
de 14 en 14. Lo más importante no es para qué sirven estas fórmulas,
sino que forman una nueva familia para la que no se tiene una
explicación sobre su existencia. Mientras tratamos de descubrirla es
posible que surjan nuevas ideas que podrían ser importantes en
matemáticas.
“Lo más importante no es para qué sirven estas fórmulas de pi, sino que no se tiene una explicación sobre su existencia”.
En la película, a Ramanujan le insisten en que aporte las pruebas de sus fórmulas. ¿Tampoco se ha conseguido con algunas de las suyas?
Con
el método WZ ya he podido demostrar cuatro fórmulas, pero se desconoce
si puede servir para demostrar las demás. Encontrar un origen común para
todas las fórmulas de esta familia es un problema que están
investigando numerosos matemáticos: Wadim Zudilin, Bruce Berndt, Yifan
Yang, Chan Heng Huat… Por otra parte, en 2008 también demostré algunos
algoritmos ultrarápidos de los hermanos Jonathan y Peter Borwein para
calcular el número pi.
Después de tanto tiempo trabajando con este número, ¿qué opina sobre él?
Pi
se define como la relación entre la longitud de una circunferencia y su
diámetro, pero este número tan especial aparece en contextos
matemáticos que nada tienen que ver con el círculo. Por ejemplo, cuando
en el siglo XVII se planteó el problema de hallar el valor exacto de la
suma 1/1 + 1/4 + 1/9 + 1 / 16 + ... nadie podía imaginar que guardara
relación con pi, pero Leonhard Euler demostró cien años después que el
resultado era el cuadrado de pi partido por 6. En la familia de
fórmulas de Ramanujan este número es fruto de relaciones con integrales
elípticas, sin embargo no sabemos por qué aparece pi en mi nueva familia
de fórmulas. Como cualquier enigma matemático supone todo un desafío.
------------------------------------------------------------------------------------------------------------------------------------------
Ejemplos de fórmulas de Ramanujan y Guillera para obtener los decimales del número π
Fórmula de Ramanujan para obtener los dígitos del número π aproximadamente de 8 en 8
Fórmula de Guillera para obtener los dígitos del número π aproximadamente de 6 en 6
En este caso los seis dígitos (en realidad son 5 y pico pero se
simplifica para su mejor comprensión) del número π se van obteniendo
según se vayan considerando más términos de las sumas y restas en B. Por
ejemplo:
Si consideramos solo el 29 daría 3'14159 (el 3 cuenta como dígito)
Si ponemos el segundo término (el del 6!) daría 3'14159 265358
Si añadimos el tercero (el del 12!) daría 3'14159 265358 979323
Y así sucesivamente…
Si consideramos solo el 29 daría 3'14159 (el 3 cuenta como dígito)
Si ponemos el segundo término (el del 6!) daría 3'14159 265358
Si añadimos el tercero (el del 12!) daría 3'14159 265358 979323
Y así sucesivamente…
De matemático autodidacta a profesional
Jesús Guillera (Zaragoza, 1955) se licenció en Ciencias Físicas en la universidad de su ciudad natal en 1979. Durante bastantes años impartió clases en institutos de bachillerato y enseñanza secundaria, pero acabó desilusionado. En el año 2007 termina su tesis basada en artículos que ya había publicado y traducido al español en formato de libro. Obtuvo la calificación de Sobresaliente Cum Laude y Premio Extraordinario en Matemáticas. Sus directores fueron Eva Gallardo (especialista en espacios de Hardy) y el matemático ruso Wadim Zudilin. Este año le han nombrado Colaborador Extraordinario del Departamento de Matemáticas de la Universidad de Zaragoza. En su página web ofrece información sobre sus trabajos, así como vídeos divulgativos en un canal de YouTube.
Fuente
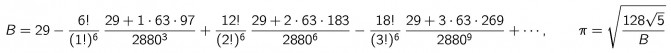
No hay comentarios:
Publicar un comentario